これは、ここをクリックした先のページの問題の解答です。
【問1】
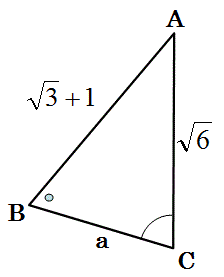
上図の三角形ABCの長さaを求めよ。
【楽な解き方】
先ず、以下の補助線を引く。
長さCDと高さhを計算する。
計算した長さCDと高さhをの値を図に書き込む。
次に、長さABを計算する。
計算した長さABの値を図に書き込む。
次に長さBDを計算する。
これで、a=長さBC=2が求められた。
(解答おわり)
【もっと楽な解き方】
下図のように、正弦定理で長さcを計算します。
cをこの式で計算するために、sinBとsinCを計算します。
sinBとsinCを使って、cを計算する。
計算結果の長さcを図に書き込む。
次に補助線ADを引く。
次に、BDとDCの長さを計算する。
(解答おわり)
【なぜ、残りの∠Aのコサインが分からないのか】
∠Bと∠Cが分かっているので、残りの角Aが、
∠A=π-∠B-∠C
で直ぐに分かるハズです。
「この問題では、なぜ、三角形の残りの角である∠Aのサインかコサインが直ぐにわからないのか?」
と、この問題の解き方に理不尽さを感じたと思います。
残りの角Aについては、
という公式があります。
これは、「加法定理」と呼ばれていて、
高校2年で学びます。
高校2年で学ぶ内容ではありますが、参考のために、上の解答の解き方を繰り返すことでsinAに関する加法定理を証明してみます。
(証明開始)
正弦定理を使って上図のcとaをbであらわします。
(証明おわり)
(補足)加法定理が上の解答の解き方を利用して導けたので、上の解き方こそ、加法定理の基礎である、大切な意味を持つことが分かります。
【2角がわかっているその他の問題の解】
cosBとcosCが分かっていて、どれか1辺の長さが決まっている問題の場合:
先ず、以下の三角形の3辺の比を計算する。
その結果得た3辺の長さの比を使って残り2辺の長さを定める。
更に、sinAも求める必要がある場合は:
(1)辺の長さbの値とsinBの値を使って半径の長さRを計算する。
(2)辺BCの長さaと、
sinA=a/(2R)
【問1】
【楽な解き方】
先ず、以下の補助線を引く。
長さCDと高さhを計算する。
次に、長さABを計算する。
計算した長さABの値を図に書き込む。
次に長さBDを計算する。
これで、a=長さBC=2が求められた。
(解答おわり)
【もっと楽な解き方】
下図のように、正弦定理で長さcを計算します。
cをこの式で計算するために、sinBとsinCを計算します。
sinBとsinCを使って、cを計算する。
計算結果の長さcを図に書き込む。
次に補助線ADを引く。
次に、BDとDCの長さを計算する。
(解答おわり)
【なぜ、残りの∠Aのコサインが分からないのか】
∠Bと∠Cが分かっているので、残りの角Aが、
∠A=π-∠B-∠C
で直ぐに分かるハズです。
「この問題では、なぜ、三角形の残りの角である∠Aのサインかコサインが直ぐにわからないのか?」
と、この問題の解き方に理不尽さを感じたと思います。
残りの角Aについては、
という公式があります。
これは、「加法定理」と呼ばれていて、
高校2年で学びます。
高校2年で学ぶ内容ではありますが、参考のために、上の解答の解き方を繰り返すことでsinAに関する加法定理を証明してみます。
(証明開始)
正弦定理を使って上図のcとaをbであらわします。
(証明おわり)
(補足)加法定理が上の解答の解き方を利用して導けたので、上の解き方こそ、加法定理の基礎である、大切な意味を持つことが分かります。
【2角がわかっているその他の問題の解】
cosBとcosCが分かっていて、どれか1辺の長さが決まっている問題の場合:
先ず、以下の三角形の3辺の比を計算する。
更に、sinAも求める必要がある場合は:
(1)辺の長さbの値とsinBの値を使って半径の長さRを計算する。
(2)辺BCの長さaと、
sinA=a/(2R)
の式を使って、 sinAを計算する。
その場合に、
sinA=sinBcosC+sinCcosB
になることがもう分かっているので、遠回りな余分な計算をしないように工夫してsinAを計算すれば良いと思います。
【再度、加法定理を証明する】
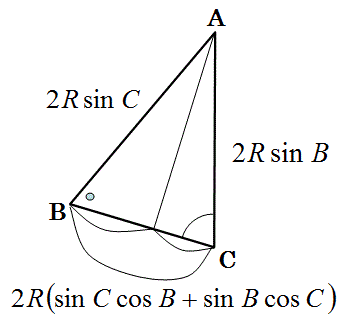
以下の様に三角形の各辺の正弦定理を使うと、加法定理が導き出されます。
そして:
sin(π-B-C)=sinC・cosB+sinB・cosC ,
sin(B+C)=sinC・cosB+sinB・cosC ,
(加法定理の導出おわり)
リンク:
高校数学の目次
その場合に、
sinA=sinBcosC+sinCcosB
になることがもう分かっているので、遠回りな余分な計算をしないように工夫してsinAを計算すれば良いと思います。
【再度、加法定理を証明する】
以下の様に三角形の各辺の正弦定理を使うと、加法定理が導き出されます。
そして:
sin(π-B-C)=sinC・cosB+sinB・cosC ,
sin(B+C)=sinC・cosB+sinB・cosC ,
(加法定理の導出おわり)
リンク:
高校数学の目次





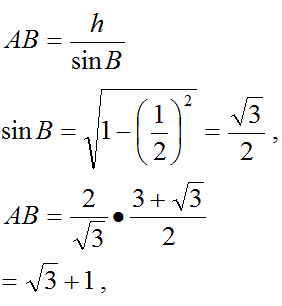














0 件のコメント:
コメントを投稿