三角形の垂心の高さの解答

これは、ここをクリックした先のページの問題の解答です。

【問１】 

 上の三角形において、垂心Ｏの高さｍが、
ｍ＝ａ１×ａ２／ｈ
であらわされることを証明せよ。

【解答】
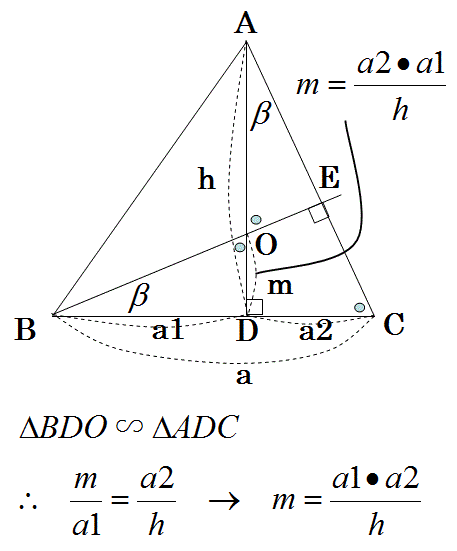
先ず、以下の様に図に同じ角度を書きこみます。

すると、三角形ＢＤＯと三角形ＡＤＣが相似であることがわかります。
その相似な三角形の辺の比が等しい式から、
垂心の高さｍを与える式が導かれます。

（解答おわり）

（補足）
　なお、辺ＣＡの長さ＝ｂ、辺ＡＢの長さ＝ｃとし、三角形ＡＢＣの外接円の半径をＲとすると、
高さｈ＝ｃ・ｓｉｎＢ
＝２ＲｓｉｎＣ・ｓｉｎＢ，
ｍ＝ｃ・ｃｏｓＢ・ｂ・ｃｏｓＣ／ｈ
＝２ＲｓｉｎＣｃｏｓＢ・２ＲｓｉｎＢ・ｃｏｓＣ／ｈ
＝２ＲｃｏｓＢｃｏｓＣ,
となり、
高さｈ＝２ＲｓｉｎＢ・ｓｉｎＣ，
　　ｍ＝２ＲｃｏｓＢ・ｃｏｓＣ,
という対称的な関係があります。
三角形の垂心の関係線分の長さは、以下の図の様に、三角比で表す長さのデパートになっています。

また、この三角比であらわす長さのデパートから、
以下の公式が成り立っていることも分かります。
ｃｏｓＡ＝ｓｉｎＢｓｉｎＣ－ｃｏｓＢｃｏｓＣ
この公式は、高校２年で学ぶ三角関数の加法定理をあらわしています。

リンク：
高校数学の目次