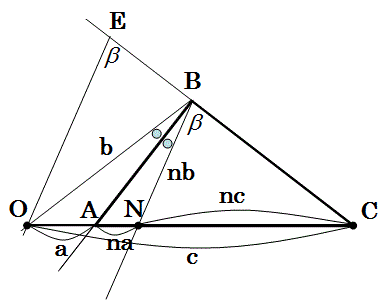
線分ONのO点とN点からの距離の比がつねに1:n である下の図の点A,B,Cは、線分OBの長さbが何であっても同一円(アポロニウスの円)の円周上にあることを証明せよ。
(コメント)アポロニウスの円を高校1年生が証明しようとすると、高校2年で学ぶ円の方程式は使わない図形の証明問題を解かなければならないと思います。
その証明の仕方を教わらないでアポロニウスの円を覚えるというのは数学のセンスを持つ学生には耐えられないことだと思います。
そのため、以下の解答の証明をしました。
【解答】
OA:NA=OB:NB=1:n
であるので、
三角形OBNにおいて、∠OBNは線分BAで二等分される。
ここで、三角形CNBに相似な三角形COEを書く。
ここで三角形COEの辺OEの長さは、
OE=c×NB/NC
=c×(b/c)
=b
になる。
三角形OEBは2辺が等しいので二等辺三角形である。
よって∠OBE=∠OEB=β
線分ABが線分ECと交叉する角度は、
∠ABE=∠ABC
である。
よって、
∠ABC=∠R=90°
である。
三角形ABCの∠B=∠Rであるので、三角形ABCは∠Bが直角である直角三角形である。
直角三角形ABCの外接円において、
辺ACに対する点Bの円周角は一定値であり90°である。
よって、点BはACを直径とする円の円周上にある。
直角三角形ABCの外接円において、
辺ACに対する点Bの円周角は一定値であり90°である。
よって、点BはACを直径とする円の円周上にある。
ゆえに、点Bは、線分OBの長さbが何であっても変わらない、線分ACを直径とする円の円周上にある。
(証明おわり)





0 件のコメント:
コメントを投稿