これは、ここをクリックした先のページの問題の解答です。
【問１】
三角形ＡＢＣの３辺の長さが上図の値の場合に、３つの頂角を求めよ。
【解１】
先ず、３辺の２乗を使う余弦定理を用いて、１つの角度のコサインを計算する。
これで、∠Ａ＝４５°であることが求められた。
他の角度の計算方針は：
（１）また余弦定理を使って他の角を計算するのは、同じ手間がかかる。もっと楽をしたい。
（２）角度Ａが分かったことを最大限に利用して、
以下の様に、Ａを頂点にする直角三角形を書き加えて長さを書きこむ。
その長さを利用して他の角度を速やかにもとめる。
上図の様に、角Ａ（あるいは角Ａの外角）を１つの頂角とし、
その辺上に点Ｂを含む直角三角形を描く。
そうすれば、角Ｂがすぐわかる様になる。
この図を見ると
ｃｏｓ（１８０°－∠Ｂ）＝１／２
である。そのため、
１８０°ー∠Ｂ＝６０°だとわかる。
どんどん図に書き込んでいく。
これで全ての角度が速やかに求められた。
（解１おわり）
《補足》
角Ｂが最初に求められた場合も、
下図の様に、角Ｂの外角を１つの頂角とし、
その辺の延長線上に点Ａを含む直角三角形を描く。
そして、その直角三角形の各辺の長さを書く。
そうすれば、角Ａがすぐわかる様になる。
【解２】２番目に簡単な解き方
最初に余弦定理を使うのも面倒なので、以下の図の様に直角三角形ＡＤＣを書き加えて、その直角三角形の各辺を、方程式で求める。
こうして、簡単な１次方程式で１つの長さが求められた。
（注意）
上の方程式の計算は、「拡張三平方の定理」を再度導出しているだけです。そのため、上の方程式の代わりに拡張三平方の定理を使って計算しても良い。
こうして１つの長さが求められたので、それを使って、他の長さも計算して図に書き加える。
この図の直角三角形ＢＤＣの辺の長さから、
∠Ｂ＝１２０°
が求められ、
直角三角形ＡＤＣの辺の長さから、
∠Ａ＝４５°
が求められた。
残りの頂角Ｃは、
∠Ｃ＝１８０°－∠Ａ－∠Ｂ
＝１５°
（解２おわり）
【解３】一番簡単な解き方
三角形の辺の２乗の引き算の公式（根元的な公式）を使って、以下のように解くこともできる。
（解３おわり）
【問２】
三角形ＡＢＣの３辺の長さが上図の値の場合に、３つの頂角を求めよ。
【解答】
この問題も一番簡単な解き方で解きます。
追加する直角三角形の直角頂点Ｄは、複雑な式で書かれている辺（の延長線）上に置くと良いようです。
（注意）
上の方程式の計算は、「拡張三平方の定理」を再度導出しているだけです。そのため、上の方程式の代わりに以下の形の余弦定理を使って計算しても良い。
上の図の各直角三角形の辺の値から、
∠Ａ＝４５°
∠Ｂ＝６０°
∠Ｃ＝１８０°ー∠Ａ-∠Ｂ＝７５°
（解答おわり）
【別解】
この問２の解き方で、Ｄ点以外の点を設定して計算を始めたらどうなるかという疑問があると思います。
その場合に、どういう計算をすれば良いかの解答例を以下に書きます。
上図のようにＥ点を設定して計算して行き、
途中で、やはりＤ点を設定して計算した方が良かったと気付いて、計算の方向を修正して、
その計算の軌道修正をしてもほとんど無駄の無い計算を行う方法を示します。
（解答開始）
余弦定理から：
上図の計算で長さＡＥを計算した答えが複雑だったので、
計算の軌道修正をして長さＡＤも計算しました。
ＡＤの計算では、ＡＥを計算した途中結果を使って速やかに計算ができました。
上図の様にＡＥの値とＡＤの値を図に書き込むと、ＢＤの長さが簡単なので∠Ｂは簡単な角度になることが分かります。
それで、∠Ｂを求めるために長さＤＢを計算します。
ＤＢ＝１なので、∠Ｂの値が簡単に求められ、
∠Ｂ＝６０°
がわかります。
また、ＡＤ＝√３なので、
∠Ａ＝４５°
もわかります。
残りの角度の、
∠Ｃ＝１８０°ー∠Ａ－∠Ｂ＝７５°
です。
（解答おわり）
（補足１）
この別解では、長さＡＤ、ＢＤ、ＣＥを求めましたので、補助に作成した直角三角形の辺の長さの関係を使って全ての頂点の角度が計算できます。
このことから、複雑な式で長さがあらわされた辺ABに対向する頂点C以外の頂点A、Bのどちらに注目しても良い。頂点Aから計算を始めても、頂点Bから計算を始めても、この別解の計算をすれば、全ての頂点の角度が楽に計算できることが分かります。
すなわち、計算を楽にするためには、
(1)複雑な式で長さがあらわされた辺ＡＢのどちらかの頂点Ａ又はＢに注目して計算を始めて、
(2)辺ＡＢを含む直線上に頂点Ｃから垂線を下ろして交点Ｄを設定する、
ことが計算が一番楽な計算になる、良い計算方針だと思います。
（補足２）
補助線を利用する解き方を高校生が知ると、毎回この解き方で解き、余弦定理を使わないので、余弦定理を覚えさせるためにこの解き方は高校の先生には望まれていないようです。
しかし、真剣勝負の場では、すなわち大学受験や、校外の模擬試験では、もちろん楽な解き方の方が良いので大いに使ってください。
また、余弦定理を覚える（導き出す）には補助線が以下の図の線分ＣＤの様に係ってきますので、補助線が本質的に大切ですので、補助線を使う作業を大切にしてください。
（余弦定理の導出）
（余弦定理の導出おわり）
以上の計算の様に、補助線CDを使って２つの直角三角形を作り、それらを利用して余弦定理を導きます。
（余弦定理の導出（その２））
計算の途中の式を、三角形の辺の二乗の引き算の公式として覚えて、以下の図と式を書いて拡張三平方の定理を思い出したら良いと考えます。
（以上が、拡張三平方の定理）
【三角形の辺の二乗の引き算の公式】
（以上が、三角形の辺の二乗の引き算の公式）
この、三角形の辺の二乗の引き算の公式は、以下の図の正方形①②③を心が思い描いて心が公式を導き出すので、覚え易い（導き出し易い）です。
（公式を自力で導き出す勧め）
覚えた定理は時が経つと忘れてしまいます。
最初教えられた時には覚えていたのに、時がたつと忘れている事に気づき、最初に覚えた記憶が戻らない。ただ覚えているだけの公式を何回思い出しても、だんだん記憶が劣化し思い出した公式に疑問を抱き公式を忘れていきます。
新しい公式を知ると、その新しい公式を覚えるために、その新しい公式に似ている旧くから覚えていた公式は、新しい公式を覚える必要のため、忘れ去られます。
数学の公式は覚えられない（時が経つと忘れる）ので、公式を導き出して使う練習をしましょう。
公式を自力で導き出して再現できる学生は、自己発電ができるパソコンのようで、自力で公式を導き出す都度、公式の理解が深まり、記憶を維持するエネルギーが発電され、いつまでも記憶が保たれます。
公式を忘れないようにするには、自力で公式を導き出す作業が欠かせません。公式を使う都度、自力で導き出すことを覚えて欲しいと思います。公式を自力で導き出すために、図に補助線を書く習慣を欠かさないようにしましょう。
なお、余弦定理を思い出す毎に、以下のように、余弦定理と等価な拡張三平方の定理が、「２項の積と二乗の差との変換公式」を使って、三角形の辺の二乗の引き算の公式に変換できる事を確認することで、思い出した記憶に間違いが無い事を確認してください。
（結論）
余弦定理も、余弦定理を使って導き出すその他の定理も、等しく、三角形の辺の二乗の引き算の公式を使って導き出すようにしましょう。
リンク：
高校数学の目次
【問１】
先ず、３辺の２乗を使う余弦定理を用いて、１つの角度のコサインを計算する。
他の角度の計算方針は：
（１）また余弦定理を使って他の角を計算するのは、同じ手間がかかる。もっと楽をしたい。
（２）角度Ａが分かったことを最大限に利用して、
以下の様に、Ａを頂点にする直角三角形を書き加えて長さを書きこむ。
その長さを利用して他の角度を速やかにもとめる。
その辺上に点Ｂを含む直角三角形を描く。
そうすれば、角Ｂがすぐわかる様になる。
ｃｏｓ（１８０°－∠Ｂ）＝１／２
である。そのため、
１８０°ー∠Ｂ＝６０°だとわかる。
（解１おわり）
《補足》
角Ｂが最初に求められた場合も、
下図の様に、角Ｂの外角を１つの頂角とし、
その辺の延長線上に点Ａを含む直角三角形を描く。
そして、その直角三角形の各辺の長さを書く。
そうすれば、角Ａがすぐわかる様になる。
【解２】２番目に簡単な解き方
最初に余弦定理を使うのも面倒なので、以下の図の様に直角三角形ＡＤＣを書き加えて、その直角三角形の各辺を、方程式で求める。
こうして、簡単な１次方程式で１つの長さが求められた。
（注意）
上の方程式の計算は、「拡張三平方の定理」を再度導出しているだけです。そのため、上の方程式の代わりに拡張三平方の定理を使って計算しても良い。
∠Ｂ＝１２０°
が求められ、
直角三角形ＡＤＣの辺の長さから、
∠Ａ＝４５°
が求められた。
残りの頂角Ｃは、
∠Ｃ＝１８０°－∠Ａ－∠Ｂ
＝１５°
（解２おわり）
【解３】一番簡単な解き方
三角形の辺の２乗の引き算の公式（根元的な公式）を使って、以下のように解くこともできる。
（解３おわり）
【問２】
【解答】
この問題も一番簡単な解き方で解きます。
追加する直角三角形の直角頂点Ｄは、複雑な式で書かれている辺（の延長線）上に置くと良いようです。
（注意）
上の方程式の計算は、「拡張三平方の定理」を再度導出しているだけです。そのため、上の方程式の代わりに以下の形の余弦定理を使って計算しても良い。
∠Ａ＝４５°
∠Ｂ＝６０°
∠Ｃ＝１８０°ー∠Ａ-∠Ｂ＝７５°
（解答おわり）
【別解】
この問２の解き方で、Ｄ点以外の点を設定して計算を始めたらどうなるかという疑問があると思います。
その場合に、どういう計算をすれば良いかの解答例を以下に書きます。
途中で、やはりＤ点を設定して計算した方が良かったと気付いて、計算の方向を修正して、
その計算の軌道修正をしてもほとんど無駄の無い計算を行う方法を示します。
（解答開始）
余弦定理から：
計算の軌道修正をして長さＡＤも計算しました。
ＡＤの計算では、ＡＥを計算した途中結果を使って速やかに計算ができました。
それで、∠Ｂを求めるために長さＤＢを計算します。
∠Ｂ＝６０°
がわかります。
また、ＡＤ＝√３なので、
∠Ａ＝４５°
もわかります。
残りの角度の、
∠Ｃ＝１８０°ー∠Ａ－∠Ｂ＝７５°
です。
（解答おわり）
（補足１）
この別解では、長さＡＤ、ＢＤ、ＣＥを求めましたので、補助に作成した直角三角形の辺の長さの関係を使って全ての頂点の角度が計算できます。
このことから、複雑な式で長さがあらわされた辺ABに対向する頂点C以外の頂点A、Bのどちらに注目しても良い。頂点Aから計算を始めても、頂点Bから計算を始めても、この別解の計算をすれば、全ての頂点の角度が楽に計算できることが分かります。
すなわち、計算を楽にするためには、
(1)複雑な式で長さがあらわされた辺ＡＢのどちらかの頂点Ａ又はＢに注目して計算を始めて、
(2)辺ＡＢを含む直線上に頂点Ｃから垂線を下ろして交点Ｄを設定する、
ことが計算が一番楽な計算になる、良い計算方針だと思います。
（補足２）
補助線を利用する解き方を高校生が知ると、毎回この解き方で解き、余弦定理を使わないので、余弦定理を覚えさせるためにこの解き方は高校の先生には望まれていないようです。
しかし、真剣勝負の場では、すなわち大学受験や、校外の模擬試験では、もちろん楽な解き方の方が良いので大いに使ってください。
また、余弦定理を覚える（導き出す）には補助線が以下の図の線分ＣＤの様に係ってきますので、補助線が本質的に大切ですので、補助線を使う作業を大切にしてください。
（余弦定理の導出）
以上の計算の様に、補助線CDを使って２つの直角三角形を作り、それらを利用して余弦定理を導きます。
（余弦定理の導出（その２））
計算の途中の式を、三角形の辺の二乗の引き算の公式として覚えて、以下の図と式を書いて拡張三平方の定理を思い出したら良いと考えます。
【三角形の辺の二乗の引き算の公式】
この、三角形の辺の二乗の引き算の公式は、以下の図の正方形①②③を心が思い描いて心が公式を導き出すので、覚え易い（導き出し易い）です。
覚えた定理は時が経つと忘れてしまいます。
最初教えられた時には覚えていたのに、時がたつと忘れている事に気づき、最初に覚えた記憶が戻らない。ただ覚えているだけの公式を何回思い出しても、だんだん記憶が劣化し思い出した公式に疑問を抱き公式を忘れていきます。
新しい公式を知ると、その新しい公式を覚えるために、その新しい公式に似ている旧くから覚えていた公式は、新しい公式を覚える必要のため、忘れ去られます。
数学の公式は覚えられない（時が経つと忘れる）ので、公式を導き出して使う練習をしましょう。
公式を自力で導き出して再現できる学生は、自己発電ができるパソコンのようで、自力で公式を導き出す都度、公式の理解が深まり、記憶を維持するエネルギーが発電され、いつまでも記憶が保たれます。
公式を忘れないようにするには、自力で公式を導き出す作業が欠かせません。公式を使う都度、自力で導き出すことを覚えて欲しいと思います。公式を自力で導き出すために、図に補助線を書く習慣を欠かさないようにしましょう。
なお、余弦定理を思い出す毎に、以下のように、余弦定理と等価な拡張三平方の定理が、「２項の積と二乗の差との変換公式」を使って、三角形の辺の二乗の引き算の公式に変換できる事を確認することで、思い出した記憶に間違いが無い事を確認してください。
（結論）
余弦定理も、余弦定理を使って導き出すその他の定理も、等しく、三角形の辺の二乗の引き算の公式を使って導き出すようにしましょう。
リンク：
高校数学の目次
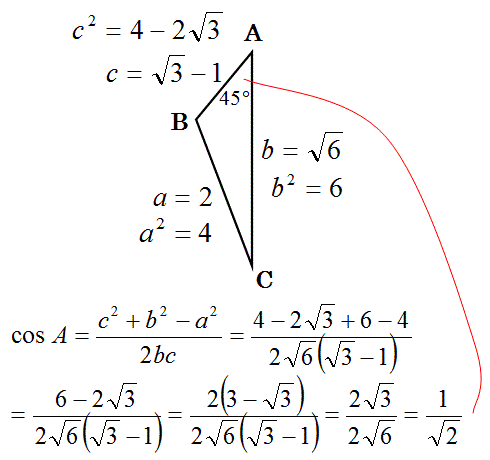
0 件のコメント:
コメントを投稿